Quality |
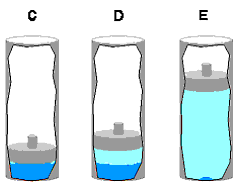
At this point we will focus on the two-phase vapor-liquid region, since most problems in introductory thermodynamics courses involve vapors and liquids. It turns out that we need one additional property for use in the two-phase region. To see why, consider the Tv diagram to the right. Suppose we specify the pressure P as the pressure along the isobar shown and consider only the superheated vapor region. Just specifying P is not enough to fix T. By specifying P we know only that the state lies somewhere on the blue part of the isobar. To find T, we would also have to specify specific volume v. We should have known this anyway because we saw on page two that it takes specification of two intensive properties to fix a state in a single phase region. Now suppose we specify the pressure at P and restrict ourselves to the two-phase region. Now we know the temperature is Tb because pressure and temperature have a one-to-one relation in the two phase region. However, specifying P in the two phase region does not fix specific volume v - it could be any number between vf and vg. In other words, many different states can exist at the same temperature and pressure in the two-phase region. To help us determine where inside the two phase region our state lies, we will define a new parameter called the quality. Before defining quality though, we need to discuss one more concept. The figure below shows several steps of our piston-cylinder experiment, specifically those inside the two phase region.
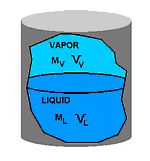
Remember that the liquid in C was called saturated liquid and the vapor in E was called saturated vapor. Recall also that the experiment was done at constant pressure and that temperature did not change as the system evolved from state C to E. Now focus for a moment only on the liquid phase as the system moves from C to E: Since neither T or P is changing, and since specifying two properties of a single phase fixes the rest, it must follow that the specific volume of the liquid remains constant from C to E as well. Since the specific volume of the saturated liquid in state C was defined as vf, it follows that the specific volume of the liquid phase is equal to vf all the way between C and E. By the same argument, the specific volume of the vapor between states C and E is always equal to the saturated vapor specific volume vg. In other words: In the two phase region, the liquid phase is always saturated liquid and the vapor phase is always saturated vapor. The two phase mixture is simply a mixture of saturated liquid and saturated vapor. The reason that the volume of the system changes from state C to E is because vg is much larger than vf. (Remember, specific volume is the reciprocal of density and densities of vapors are much smaller than those of liquids.) When a unit mass of liquid vaporizes, it therefore requires a larger volume and the piston rises to accomodate it. Now we are in a position to define quality. Consider the closed vessel below which contains a mixture of vapor and liquid of a pure substance.
The vapor has mass Mv and a total volume Vv. Likewise, the liquid phase has mass ML and total volume VL. The total mass M of material in the vessel is the sum of the masses of the vapor and liquid phases: (1) M = ML + MV Likewise, the total volume V of the vessel is the sum of the volumes of the two phases: (2) V = VL + VV Earlier, we showed that the relation between specific volume v and total volume V is given by (3) V = vM Now consider the liquid phase. As we discussed above, the specific volume of the liquid, when two phases are present, will always be vf. Therefore we can say that (4) VL = vfML By the same argument, we can write for the vapor phase: (5) VV = vgMV
Substituting (3), (4) and (5) into (2) followed by dividing through by M and then eliminating M using equation (1) yields: (6) v = {MV/(MV + ML)}vg + {ML/(MV + ML)}vf
At this point the quality x is defined as
(7) x = MV/(MV + ML)
Note that quality is nothing other than the fraction of the total mass in a vapor-liquid system that is in the vapor phase. Since state C of our experiment was all saturated liquid, its quality is zero. State E was all saturated vapor (all of the mass in the system was vapor) so its quality would be one. All states intermediate between C and E would have a quality between zero and one.
Substituting equation (7) into (6) yields:
(8) v = x vg + (1-x) vf
which provides a relation between specific volume v and quality x in the two phase region. Note when x=0, equation (8) says that v=vf. Likewise, when x=1, v=vg. Thus, any point on the saturated liquid curve has quality zero and any point on the saturated vapor curve has a quality of one. Points inside the two phase region will have a quality between zero and one. In closing this section, we should note that a common mistake is to use quality in a single phase region. However, quality is not needed in the single phase regions because there is never any difficulty in determining a specific volume for a given temperature and pressure. It is only in the two phase regions, where many different states can exist at the same temperature and pressure, that an additional variable is needed. So remember: Quality is only defined for two phase regions! Important Points:
x = MV/(MV + ML) and is the fraction of the total mass that is in the vapor phase.
v = x vg + (1-x) vf
This concludes the material for this tutorial. Now it is time to test yourself to see if you were able to absorb all of the material. On the following pages are three quizzes (one on the PT diagram, one on the Tv diagram, and one on general topics). Take them to identify any concepts that you need to revisit.
Next page Previous page Contents page Exit tutorial
|