Pressure-Volume-Temperature Relation

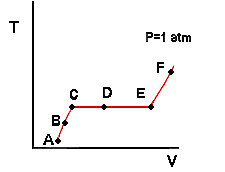
While there are a number of different properties that important in the field of thermodynamics, the focus of this tutorial is on pressure, specific volume and temperature of a pure substance.  This is a good starting point because we can imagine how each of these intensive properties could be measured.  All we need is a pressure gauge, a thermometer, a ruler (to measure volume) and a scale (to measure mass so we can calculate specific volume).  As you will see later, not all thermodynamic properties are as easily obtained.

Another reason to focus on pressure, specific volume and temperature is that they form the simplest set of variables from which a phase diagram can be constructed -  and gaining an understanding of phase diagrams is the point of this tutorial.

On the previous page, we discussed how, for a single phase, specifying two intensive properties fixed the rest.  Therefore, we can think of specific volume, pressure and temperature as forming a relation (called the Pressure-Volume-Temperature or PvT relation) between two independent variables and a dependent one.  Which of these properties we consider to be the dependent one will depend on the problem we are trying to solve.

The easiest way to understand the PvT relation is to generate it by a thought experiment.   Consider the piston-cylinder shown under letter A to the right.  Imagine that we have placed some liquid water in the cylinder and sealed it with the piston ensuring that no air is present with the water.   (You may want to exercise your creative muscles and come up with an idea for how you might practically accomplish this.)  We will assume the piston to be freely floating (no friction between the piston and the cylinder).  Now we place the entire assembly in a constant temperature bath at 100 degrees Fahrenheit and let the system equilibrate.  We will assume that the pressure of the water in the cylinder is exactly one atmosphere (1 atm).  You may be thinking that this is not possible because the pressure of the water will equal the pressure of the external atmosphere plus the additional pressure generated by the weight of the piston.  This is a thought experiment though so we can cook up some way to make the pressure of the water equal to one atmosphere.  For instance, we could imagine that the entire assembly is in an evacuated chamber and the mass of the piston is chosen so as to produce a pressure of exactly 1 atm on the water.

Now we add heat to the piston-cylinder assembly by increasing the bath temperature.  Let us suppose we increased the temperature to 200 degrees Fahrenheit.  What will happen to the temperature of the water in the cylinder?   We would observe that it would increase until it reached equilibration with the bath temperature as shown in drawing B.  What about the pressure of the water?   This might be a little tricky:  It would remain constant because the piston is freely floating.  Take some time to convince yourself of this.  Hint:  Do a force balance at the interface between the piston and the water.  What are the forces acting downward?  Have any of these changed when we added heat to the water?  If not, will the upward force (caused by the pressure of the water) change?

We note also that the volume of the water increased (reflected by the rise of the piston) as our system evolved from point A to B.  Since the mass of water is constant, this means that its specific volume must have increased.  Why?   Because it is observed that liquids expand as temperature is increased at constant pressure.

Now suppose we change the bath temperature to 220 degrees.   What will happen?  The pressure will remain constant and the temperature of the water will begin to rise so as to equilibrate with the bath temperature.   Therefore the volume (and specific volume) of the water will increase as well.  We make a curious observation though.  When the water temperature reaches 212 degrees (on its way to 220) we observe a small bubble of water vapor form (Figure C). 

In these drawings, dark blue represents liquid water and light blue represents water vapor.

Now heat continues to flow into the water from the bath because the water is still at a lower temperature.  However, we observe that the temperature of the water in the cylinder does not change.  Also, we notice that the volume continues to increase but not because the temperature is changing.  Rather it increases because the liquid is vaporizing and the specific volume of vapor is larger than that of liquid.  This vaporization of water is illustrated by Figures C, D and E to the right.

Imagine now that Figure E represents the point at which the last small drop of liquid vaporizes.  What will happen at this point?  Now the water is all vapor and it will behave similarly to as it did when it was all liquid:  The temperature of the water vapor will begin to rise (at constant pressure) and will continue to rise until it reaches 220 degrees (Figure F).  The volume (and specific volume) will increase because gases expand as temperature is increased at constant pressure. 

Note that there were three distinct parts to this experiment:   One in which the water was entirely liquid, one in which it was entirely vapor, and one in which two phases were present.

We can imagine plotting our results on a diagram of temperature T versus specific volume v.  Each point A through F would be plotted and then connected by a line.  For points in which two phases were present, we will simply divide the total volume inside the piston-cylinder by the total mass of water (liquid+vapor).  The specific volume that we obtain in this manner would be an average value and would be intermediate to the specific volumes of the individual vapor and liquid phases.

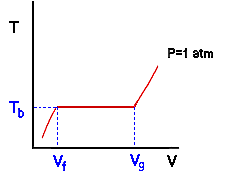
Note that every point on the red line (which represents the continuum of states that the water passed through) is at the same pressure of 1 atmosphere.  We call this line an isobar or line of constant pressure.   Take a minute to convince yourself that the line from A to C represents liquid water, from C to E represents two phase behavior, and from E to F represents water vapor.   We will call a diagram of this type a Temperature-Volume or Tv diagram.  Tv diagrams show the relation between temperature and specific volume along lines of constant pressure (isobars).

Now some nomenclature.  Imagine that state C represents the point at which the water is entirely liquid but the first very small bubble of vapor is just about to form.  The water in this state is called saturated liquid.   Likewise, imagine that state E represents the point at which the last drop of liquid has just disappeared and the system is entirely vapor.  The water vapor in this state is called saturated vapor.  In this context, saturated means that a single phase is right at the point of becoming two phases.  The specific volumes of the saturated liquid water in C and the saturated water vapor in E are given the symbols v_f and v_g respectively.

Note that the horizontal portion of the isobar corresponds to the part of the experiment in which two phases were present.  We observed that the temperature remained constant at 212 degrees.  The temperature at which  liquid and vapor phases of a pure substance coexist at a given pressure is called the boiling temperature T_b at that pressure.  Thus the boiling temperature of water is 212 degrees Fahrenheit at a pressure of 1 atm.

This leads to an important point that we will return to several times:  For those states in which liquid and vapor were present at the same pressure, the temperature was always the same value and is called the boiling temperature.   Thus, the boiling temperature of a pure substance depends only on the pressure and not on the specific volume.  To put it another way:  When vapor and liquid phases are present, there is a one to one relationship between temperature and pressure.  Specifying one fixes the other.

Note that this is different from what happens in a single phase where both pressure and specific volume (two intensive variables) would have to be specified in order to fix the temperature.  We will find later that the same thing happens when we have coexisting solid and liquid phases and coexisting solid and vapor phases.

The specific volumes of the saturated liquid and saturated vapor, along with the boiling temperature, are illustrated for our experiment in the next drawing:

Important Points:

• The PvT relation provides the relationship between pressure, specific volume, and temperature.

• In a single phase, two of these properties must be specified in order to fix the third.

• When both liquid and vapor phases are present, there is a one-to-one relationship between temperature and pressure.  The temperature when two phases are present is called the boiling temperature.

• Saturated liquid refers to a liquid that is at the point of forming a vapor phase.  Saturated vapor is vapor that is at the point of forming a liquid phase.

• An isobar is a line of constant pressure.

• a Temperature-Volume (Tv) diagram shows the relation between temperature and specific volume along isobars.

One of the advantages of Web-based tutorials is that they allow for animation.  The static description of the thought experiment given here may be easier to visualize in an animated form.  The animated version of the experiment is given on the next page.   Spend a few minutes with it to fix the ideas presented on this page.

  Next page                 Previous page                  Contents page                   Exit tutorial