Generating the Tv Diagram |
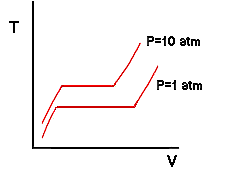
On the previous page, we used a thought experiment involving a piston-cylinder assembly to trace the behavior of temperature vs specific volume for water at a pressure of one atmosphere. Now we will examine what happens at other pressures. Suppose that we were to throw some weights on the piston so as to make the pressure of the water equal to 10 atmospheres. Then we repeat the experiment. What do you think would happen? Ask yourself first what would happen to the boiling temperature: would it increase or decrease? It turns out it would increase. In other words, boiling temperature increases with increasing pressure and decreases with decreasing pressure. Any of you that have tried to cook food in boiling water while camping in the mountains (lower atmospheric pressure) have probably observed that the water boils at a lower temperature. So if pressure is increased from 1 atm to 10 atm, the boiling temperature of the water would increase and our isobar for the new experiment might be expected to look like this:
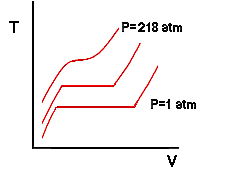
Notice that in addition to an increase in boiling temperature there is also a change in the specific volumes of the saturated liquid and vapor. The fact that the boiling temperature of a substance depends on pressure may seem counter-intuitive to those of you that are used to hearing that the boiling temperature of water is 212 degrees Fahrenheit. This is a result of sloppy semantics. The boiling temperature of a pure substance at a pressure of 1 atm is called the normal boiling temperature. So the correct usage is that the boiling temperature of water depends on the pressure but the normal boiling temperature of water is 212 degrees Fahrenheit. We are on a run now so let's add more weight to the piston and do the experiment again. In fact, let's assume that we have added weight to the piston such that the pressure of the water is 218 atmospheres. We would observe a curious result: At no point would we ever observe two phases inside the cylinder. The isobar of the process is shown by the 218 atm line in the next drawing and it would have the characteristic that it becomes flat at only one single point - a horizontal inflection point:
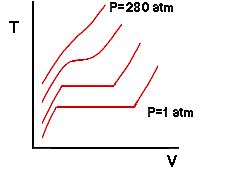
If were to add even more weight, say enough to generate a pressure of 280 atmospheres on the water, we would obtain an isobar that was not flat at even a single point:
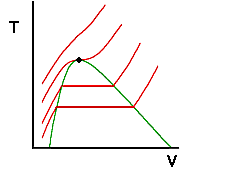
Whats going on here? It turns out for water that 218 atm is the highest pressure for which a liquid and a vapor can coexist (and there only at the single point in which the isobar is flat) . For any higher pressure, water will always be in a single phase - no matter what the temperature or specific volume are. Recall that the flat regions of the isobars correspond to states for which vapor and liquid coexist. Also, we know that the ends of these flat regions correspond to saturated liquid and saturated vapor states. We can connect the locus of all saturated liquid states and saturated vapor states to show the region where two phases are present:
Note that for any state inside the green dome, vapor and liquid are both present. Anywhere outside the dome, only a single phase is present. Note also that the isobar that became flat at a single point coincides with the highest point of the two-phase dome. We know that the region to the left of the dome is liquid and the region to the right is vapor but what happens above the dome? And if we were to follow the highest isobar in the drawing above from its lowest temperature to its highest, would that not suggest that we have moved from liquid to vapor without moving through a two phase region? We will examine these questions on the next page. Before doing so, let's review the important ideas from this page.
Important Points:
Next page Previous page Contents page Exit tutorial
|